The Mathematics of Social Sciences
As I enter my journey at IIMB as a PhD candidate in marketing, I see myself as a social scientist. I see myself as an explorer and investigator of the human mind and behavior. I see myself applying principles of psychology, sociology and anthropology - the beautiful 'soft' sciences of mankind. But suddenly, my vehicle of learning takes a sharp detour into the 'hard' science of mathematics.
Over the last 3 weeks, I have been exposed to a lot of mathematics - a lot and of a different breed. I have been exposed to a lot of concepts whose existence I was oblivious to. After keeping me away from mathematical education after class 12, life decided to finally orchestrate a rendezvous with Linear Algebra. As terms like matrices, vectors, transpose, multivariate calculus, projections, etc. were being 'bombarded' at me, a volley of questions bounced in my mind...
"Why do I need to learn all this? How is this related to my future research work? How will this help me in understanding the human mind? Isn't statistics enough to compute quantitative data? Why do we need matrix algebra here???"

For the first 2 weeks, these questions kept rotating within my mind. But as I entered the third week, consciousness dawned into me. After spending 5 hours with Gilbert Strang (I met him virtually through his book!), epiphany struck its magic wand and I realized that Linear Algebra is one of the coolest things a social scientist can learn. From that moment, I started seeing myself as a potential 'Social Mathematician' as well.
As a social scientist, I would be involved in explaining the human mind and behavior. As we all know, today's world is not a very simple place. There is nothing purely black or white. There are various shades of grey. And as we all know, grey is nothing but a linear combination of black and white.
Let's take a simple generalization of the human mind being a combination of 2 elements namely - Good & Evil. All the people in this world would have different combinations of good and evil in their minds. We can draw parallels with numerous ancient oriental philosophical concepts like Yin & Yang (Combination of 2 opposing elements) and Om (Combination of 3 elements A,U,M).
So, we can start identifying linear combinations in almost everything around us, including the human mind.
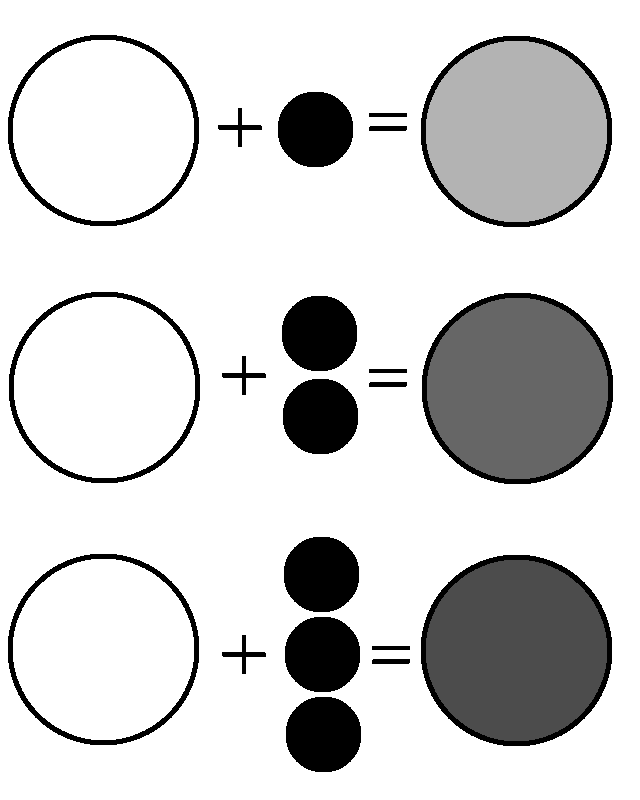
Let's go back to our basic example of linear combination of 2 basic colours - Black and White.
Now, imagine that I am mixing these 2 paints on a palette to get a resultant colour Grey. It is possible for me to mix black and white paint in different proportions to arrive at various shades of grey.

When we are given a particular shade of grey, we can find out the specific proportion of black and white that was combined to get this specific shade of grey. Since grey is a linear combination of black and white, we can express them in the form of algebraic equations where w= white, b=black and g=grey
Here, x & y are the proportional weights of white & black respectively.
For different values of x & y, I will get different shades of grey.
g= xw+yb
Here, x & y are the proportional weights of white & black respectively.
For different values of x & y, I will get different shades of grey.
We can express this particular linear combination in the form on a matrix where the rows equate to the dimension of 'whiteness' and 'blackness' and the columns signify the actual colours:
In a scenario where I am mixing only 2 elementary colors - black and white - that are mutually independent of each other - for every shade of grey I can identify the specific combination of black and white. But there may be situations where we may not be able to arrive at a specific combination.
Situation 1 - No possible combinations!
Imagine you come across a question as absurd as, "What combination of black and white will give you RED?"
No matter what combination of black and white you mix on your palette, you will never get red. Hence, such a situation has no solution.
Situation 2 - Infinite possible combinations!
Imagine you come across a question that says, "What combination of black, white and medium grey will give you dark grey?
Here, we are combining 3 colours to get a fourth colour. But the problem is that the initial 3 colours are not mutually independent of each other. The third colour medium grey is a linear combination of the first 2 colours. In such a situation, we end up getting infinite possible combinations!
Let's see this with a numeric illustration:
We define medium grey as lg= w+b, and dark grey as dg= w+3b, we can express this as:
As it can be seen above, we can have multiple possible combinations of the 3 colours to arrive at the fourth colour. We can either mix only white and black and none of medium grey, or take a portion of medium grey and add some more black to it to make it dark grey. If we were to include the possibility of having negative values (i.e, if it was possible to remove some colours from a mixture), we would be able to get infinite solutions!

Till now we looked at colours and pigments which are physical objects. But the crux of the exploration of a social scientist is human mind and behavior. So, let's apply the concept of linear combination in a human phenomena.
Let's ask a fundamental question - "What makes me content with my life?"
As a social scientist, I would think of various elements that lead to contentment in life. These elements could be having a job that you love, having a positive family life and earning handsome money.
Linear algebra comes into picture here because the level of contentment in my life would be a linear combination of these 3 elements in some proportion!
For some people, earning good money may be more important than doing something you love. Such people end up doing a job that they hate doing just because it pays them well. For some people, family happiness may be much more important than job satisfaction. Such people may end up doing something they hate just in order to keep their family happy. Instead of just guessing what element could be important in a society, we can use the magical wand of Linear Algebra to precisely find those proportions!
For illustrative purposes, let's assume that we are trying to find these proportions among a homogeneous group of 28 year old, male, graduate, working professionals in Bangalore. In order to find the combinations, we need to measure the individual elements. We can measure the following 4 questions using a 100 point scale where 0=Not at all and 100= A lot:
Q1. How content are you with your life?
Q2. How much do you like the work that you are doing?
Q3. How much higher do you think is your salary as compared to what people get at your age & experience?
Q4. How positive/ pleasant is the overall mood of your family?
We administer these questions to 3 people and their responses are as follows:
As it can be seen, the data that we receive will always be in a tabular or matrix form. Each column stands for a variable captured in a question. Since we are trying to find the importance of each variable on the final variable of Life contentment, we will carry out combination of columns as follows:
On solving this system by linear algebra methods, we arrive at the solution of x=0.3, y=0.2 and z=0.5.
This gives us the solution that family positivity is given more importance, followed by work likeability and paycheck.
With the help of linear algebra, we can find out what is the main driver of contentment. Similarly, this tool can be applied in calculating any other measurable linear combination in this world.
We know that the human brain is made up of grey cells and the human mind is also made up of shades of grey. Mathematics can be used to quantify the human mind and yes, we can calculate more than just 50 shades of grey!
Moral of the story: Embrace mathematics, even if you claim to be a qualitative researcher because beauty lies in integration - the linear combination of qualitative and quantitative research!

Linear Algebra helps us visualize beyond the physical 3 dimensional space through the column-vector concept. Once we are able to visualize multiple dimensions, we may get closer to solving Einstein's dilemma here:

As it can be seen above, we can have multiple possible combinations of the 3 colours to arrive at the fourth colour. We can either mix only white and black and none of medium grey, or take a portion of medium grey and add some more black to it to make it dark grey. If we were to include the possibility of having negative values (i.e, if it was possible to remove some colours from a mixture), we would be able to get infinite solutions!
Now, let's calculate the grey areas of human mind
Let's ask a fundamental question - "What makes me content with my life?"
As a social scientist, I would think of various elements that lead to contentment in life. These elements could be having a job that you love, having a positive family life and earning handsome money.
Linear algebra comes into picture here because the level of contentment in my life would be a linear combination of these 3 elements in some proportion!
For some people, earning good money may be more important than doing something you love. Such people end up doing a job that they hate doing just because it pays them well. For some people, family happiness may be much more important than job satisfaction. Such people may end up doing something they hate just in order to keep their family happy. Instead of just guessing what element could be important in a society, we can use the magical wand of Linear Algebra to precisely find those proportions!
For illustrative purposes, let's assume that we are trying to find these proportions among a homogeneous group of 28 year old, male, graduate, working professionals in Bangalore. In order to find the combinations, we need to measure the individual elements. We can measure the following 4 questions using a 100 point scale where 0=Not at all and 100= A lot:
Q1. How content are you with your life?
Q2. How much do you like the work that you are doing?
Q3. How much higher do you think is your salary as compared to what people get at your age & experience?
Q4. How positive/ pleasant is the overall mood of your family?
We administer these questions to 3 people and their responses are as follows:
Name
|
Work
Likeability
|
Paycheck
Handsomeness
|
Family
Positivity
|
Life
Contentment
|
Ayush
|
40
|
50
|
10
|
27
|
Bharath
|
20
|
60
|
40
|
38
|
Chandan
|
60
|
30
|
50
|
49
|
As it can be seen, the data that we receive will always be in a tabular or matrix form. Each column stands for a variable captured in a question. Since we are trying to find the importance of each variable on the final variable of Life contentment, we will carry out combination of columns as follows:
On solving this system by linear algebra methods, we arrive at the solution of x=0.3, y=0.2 and z=0.5.
This gives us the solution that family positivity is given more importance, followed by work likeability and paycheck.
With the help of linear algebra, we can find out what is the main driver of contentment. Similarly, this tool can be applied in calculating any other measurable linear combination in this world.
We know that the human brain is made up of grey cells and the human mind is also made up of shades of grey. Mathematics can be used to quantify the human mind and yes, we can calculate more than just 50 shades of grey!
Moral of the story: Embrace mathematics, even if you claim to be a qualitative researcher because beauty lies in integration - the linear combination of qualitative and quantitative research!
Linear Algebra helps us visualize beyond the physical 3 dimensional space through the column-vector concept. Once we are able to visualize multiple dimensions, we may get closer to solving Einstein's dilemma here: